Số chính phương luôn là một khái niệm thú vị trong toán học, khơi gợi sự tò mò của bao thế hệ học sinh. Bạn có bao giờ tự hỏi số chính phương là gì và tại sao chúng lại đặc biệt? Từ những con số quen thuộc như 1, 4, 9 đến các bài toán phức tạp, số chính phương xuất hiện khắp nơi trong đời sống và học thuật. Trong bài viết này, chúng ta sẽ khám phá lý thuyết, cách nhận biết, và giải bài tập về số chính phương từ dễ đến khó, giúp bạn nắm chắc chủ đề này một cách dễ dàng!
1. Số chính phương là gì?
Số chính phương là bình phương của một số tự nhiên.
2. Tính chất
Số chính phương chỉ có thể tận cùng bằng 0, 1,4, 5, 6, 9 không thể tận cùng bằng 2, 3, 7, 8.
Khi phân tích ra thừa số nguyên tố, số chính phương chỉ chứa các thừa số nguyên tố với mũ chẵn, không chứa thừa số nguyên tố với số mũ lẻ.
Hệ quả. Số chính phương chia hết cho số nguyên tố P thì phải chia hết cho ${{P}^{2}}$
Một số chính phương khi và chỉ khi số ước của nó là số lẻ.
3. Một số kiến thức khi sử dụng
Hệ thập phân
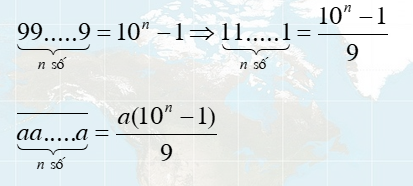
Các hằng đẳng thức.
Nếu a = b.c mà a là số chính phương; (b; c) = 1 thì b và c đều là số chính phương.
4. Bài tập
Bài tập 1: Tìm số tự nhiên n để $n+18$ và $n-41$ là các số chính phương.
Lời giải
Tìm cách giải. Để tìm số tự nhiên n thỏa mãn điều kiện trên, chúng ta đồng nhất hai điều kiện đó bằng cách đặt $n+18={{a}^{2}};\,n-41={{b}^{2}}\,\left( a;b\in \mathbb{N};a>b \right)$. Sau đó khử n bằng phép trừ vế cho vế, khi đó ta sẽ tìm được số tự nhiên a, b bằng con đường ước số.
Trình bày lời giải
Đặt $n+18={{a}^{2}};\,n-41={{b}^{2}}\,\left( a;b\in \mathbb{N};a>b \right)$
Suy ra ${{a}^{2}}-{{b}^{2}}=59\Leftrightarrow \left( a-b \right)\left( a+b \right)=59=1.59$
Do đó $\left\{ \begin{array}{l} a – b = 1\\ a + b = 59 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 30\\ b = 29 \end{array} \right. \Leftrightarrow n = 882$.
Bài tập 2: Chứng minh rằng nếu $m.n\in \mathbb{Z}$ thoả mãn đẳng thức: $3{{m}^{2}}+m=4{{n}^{2}}+n$ thì $m-n$ và $4m+4n+1$ đều là số chính phương.
Lời giải
Từ $3{{m}^{2}}+m=4{{n}^{2}}+n$ ta có $m\ge n$ và
$\Leftrightarrow 4\left( {{m}^{2}}-{{n}^{2}} \right)+m-n={{m}^{2}}$
$\Leftrightarrow \left( m-n \right)\left( 4m+4n+1 \right)={{m}^{2}}$ (*)
Đặt $\left( m-n;4m+4n+1 \right)=d$
$\Rightarrow \left( m-n \right)\vdots d;\left( 4m+4n+1 \right)\vdots d$ và $m\vdots d$
$\Rightarrow \left\{ 4m+4n+1+4\left( m-n \right) \right\}\vdots d\Rightarrow \left( 8m+1 \right)\vdots d$ mà $m\vdots d$
$\Rightarrow 1\vdots d$ hay $d=1$
Vậy $m-n$ và $4m+4n+1$ nguyên tố cùng nhau, kết hợp với (*) ta có: $m-n$ và $4m+4n+1$ đều là số chính phương.
Bài tập 3: Giả sử a là số nguyên dương và d là một ước số nguyên dương của $2{{a}^{2}}$. Chứng minh rằng: ${{a}^{2}}+d$ không thể là số chính phương.
Lời giải
Giả sử $2.{{a}^{2}}=k.d$ và ${{a}^{2}}+d={{b}^{2}}$ với $a,b,k,d\in {{\mathbb{Z}}^{+}}$.
Từ ${{a}^{2}}+d={{b}^{2}}\Leftrightarrow {{a}^{2}}+\frac{{{2}^{2}}}{k}={{b}^{2}}\Leftrightarrow {{k}^{2}}{{b}^{2}}={{a}^{2}}\left( {{k}^{2}}+2.k \right)$
$\Leftrightarrow {{\left( kb \right)}^{2}}={{a}^{2}}\left( {{k}^{2}}+2k \right)\Leftrightarrow {{k}^{2}}+2k$ là số chính phương.
Mà ${{k}^{2}}<{{k}^{2}}+2k<{{\left( k+1 \right)}^{2}}\Rightarrow {{k}^{2}}+2k$ không thể là số chính phương
Vậy ${{a}^{2}}+d$ không thể là số chính phương.
Bài tập 4: Chứng minh rằng không tồn tại số tự nhiên n thỏa mãn ${{n}^{2}}+2018$ là số chính phương.
Lời giải
Giả sử tồn tại số tự nhiên n thỏa mãn đề bài. Đặt ${{n}^{2}}+2018={{m}^{2}}$ $\left( n\in \mathbb{N} \right)$ $\Rightarrow \left( m-n \right)\left( m+n \right)=2018$ (*)
Khi đó:
+ Nếu m và n khác tính chẵn lẻ thì $\left( m-n \right)\left( m+n \right)$ lẻ, mâu thuẫn với (*).
+ Nếu m và n cùng tính chẵn lẻ thì $\left( m-n \right)\left( m+n \right)$ chia hết cho 4, mâu thuẫn với (*).
Vậy không tồn tại số tự nhiên n thỏa mãn ${{n}^{2}}+2018$ là số chính phương.
Bài tập 5: Cho hai số tự nhiên a và b. Chứng minh rằng nếu tích a.b là số chẵn thì luôn luôn tìm được số nguyên c sao cho ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ là số chính phương.
Lời giải
Ta có a.b là số chẵn, xảy ra hai trường hợp.
– Trường hợp 1. Nếu hai số cùng chẵn thì ${{a}^{2}}+{{b}^{2}}\vdots 4$ .
Đặt ${{a}^{2}}+{{b}^{2}}=4k$ $\left( k\in \mathbb{N} \right)$. Khi đó, chọn $c=k-1$.
Ta có ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=4k+{{\left( k-1 \right)}^{2}}={{\left( k+1 \right)}^{2}}$.
– Trường hợp 2. Nếu một số chẵn, một số lẻ thì ta đặt ${{a}^{2}}+{{b}^{2}}=2k+1$ $\left( k\in \mathbb{N} \right)$. Khi đó, chọn $c={{k}^{2}}$.
Ta có ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}={{\left( k+1 \right)}^{2}}$.
Vậy luôn chọn được số c sao cho ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ là số chính phương.
Bài tập 6: Nếu $a,b\in {{\mathbb{Z}}^{+}}$ thỏa mãn $2{{a}^{2}}+a=3{{b}^{2}}+b$ thì $a-b$ và $2a+2b+1$ là những số chính phương.
Lời giải
Từ $2{{a}^{2}}+a=3{{b}^{2}}+b$ ta có $a>b$ và
$\Leftrightarrow 2\left( {{a}^{2}}-{{b}^{2}} \right)+a-b={{b}^{2}}$
$\Leftrightarrow \left( a-b \right)\left( 2a+2b+1 \right)={{b}^{2}}$ (*)
Đặt $\left( a-b;2a+2b+1 \right)=d\Rightarrow \left( a-b \right)\vdots d;\left( 2a+2b+1 \right)\vdots d$ và $b\vdots d$
$\Rightarrow \left\{ 2a+2b+1-2\left( a-b \right) \right\}\vdots d\Rightarrow \left( 4b+1 \right)\vdots d$ mà $b\vdots d\Rightarrow 1\vdots d$ hay $d=1$
Vậy $a-b$ và $2a+2b+1$ nguyên tố cùng nhau, kết hợp với (*) ta có:
$a-b$ và $4a+4b+1$ đều là số chính phương.
Bài tập 7: Cho a, b, c, d là các số nguyên thỏa mãn $a\le b\le c\le d$ và $a+d=b+c$.
Chứng minh rằng ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}$ là tổng của ba số chính phương.
Lời giải
Vì $a\le b\le c\le d$ nên ta có thể đặt $a=b-k$ và $a=c+h$ (vì $h.k\in \mathbb{Z}$)
Khi đó $a+d=b+c\Leftrightarrow b-k+c+h=b+c\Rightarrow h=k$
Vậy $a=b-k$ và $d=c+k$
Do đó: ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}={{\left( b-k \right)}^{2}}+{{b}^{2}}+{{c}^{2}}+{{\left( c+k \right)}^{2}}$
$=2{{b}^{2}}+2{{c}^{2}}+2{{k}^{2}}-2bk+2ck$
$={{b}^{2}}+2bc+{{c}^{2}}+{{b}^{2}}+{{c}^{2}}+{{k}^{2}}-2bc-2bk+2ck+{{k}^{2}}$
$={{\left( b+c \right)}^{2}}+{{\left( b-c-k \right)}^{2}}+{{k}^{2}}$
Đó là tổng của ba số chính phương.
Bài tập 8: Tìm tất cả các số tự nhiên n sao cho ${{n}^{2}}-14n-256$ là số chính phương.
Lời giải
Đặt ${{n}^{2}}-14n-256={{k}^{2}}$ với $k\in \mathbb{N}$
$\Rightarrow {{\left( n-7 \right)}^{2}}-305={{k}^{2}}\Rightarrow {{\left( n-7 \right)}^{2}}-{{k}^{2}}=305\Rightarrow \left( n-k-7 \right)\left( n+k-7 \right)=305$
$\Rightarrow n-k-7;n+k-7\in \ddot{O}\left( 305 \right)=\left\{ \pm 1;\pm 5;\pm 61;\pm 305 \right\}$
Mà $n-k-7<n+k-7$ nên ta có:

Suy ra:
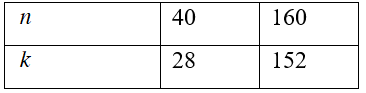
Vậy với $n\in \left\{ 40;160 \right\}$ thì${{n}^{2}}-14n-256$ là số chính phương.
Bài tập 9: Chứng minh rằng số $A=224\underbrace{99…..9}_{n-2\text{ so }\!\!\acute{\mathrm{a}}\!\!\text{ 9}}1\underbrace{00…..09}_{n\text{ so }\!\!\acute{\mathrm{a}}\!\!\text{ 0}}$ là số chính phương $\left( n\ge 2 \right)$
Lời giải
Ta có:
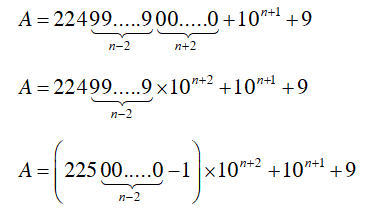
$A=\left( {{225.10}^{n-2}}-1 \right){{.10}^{n+2}}+{{10}^{n+1}}+9$
$A={{225.10}^{2n}}-{{10}^{n+2}}+{{10}^{n+1}}+9$
$A={{225.10}^{2n}}-{{90.10}^{n}}+9$
$A={{\left( 15,{{10}^{n}}-3 \right)}^{2}}$ số chính phương
Bài tập 10: Cho số nguyên dương n. Đặt $A=\underbrace{44…..4}_{2n\text{ }};\,\,B=\underbrace{88…..8}_{n}$
Chứng minh rằng $A+2.B+4$ là số chính phương
Lời giải
Ta có: $A=\underbrace{44…..4}_{2n\text{ }}=4.\underbrace{11…..1}_{2n\text{ }}=4.\frac{{{10}^{2n}}-1}{9}$
$B=\underbrace{88…..8}_{n}=8..\underbrace{11…..1}_{2n\text{ }}=8.\frac{{{10}^{n}}-1}{9}$
Xét $A+2B+4=\frac{4\left( {{10}^{2n}}-1 \right)}{9}+\frac{2.8\left( {{10}^{n}}-1 \right)}{9}+4$
$=\frac{{{4.10}^{2n}}-{{4.16.10}^{n}}-16+36}{9}$
$=\frac{4.\left( {{10}^{2n}}-{{4.10}^{n}}+4 \right)}{9}={{\left[ \frac{2\left( {{10}^{n}}+2 \right)}{3} \right]}^{2}}=\underbrace{{{\left( 66…68 \right)}^{2}}}_{n-1}$
Ta có điều phải chứng minh.
Bài tập 11: Cho $a=\underbrace{11…..1}_{2n\text{ }};\,\,b=\underbrace{44…..4}_{n}$. Chứng minh rằng $a+b+1$ là số chính phương.
Lời giải
Ta có: $a=\frac{{{10}^{2n}}-1}{9};b=\frac{4\left( {{10}^{n}}-1 \right)}{9}$
Đặt ${{10}^{n}}=x\Rightarrow a=\frac{{{x}^{2}}-1}{9};b=\frac{4\left( x-1 \right)}{9}$
$a+b+1=\frac{{{x}^{2}}-1+4x-4+9}{9}={{\left( \frac{x+2}{3} \right)}^{2}}$
Mà $x+2=10…02\vdots 3\Rightarrow a+b+1$ là số chính phương.
Bài tập 12: Cho $A=\underbrace{11…..1}_{2n\text{ so }\!\!\acute{\mathrm{a}}\!\!\text{ 1}};\,\,B=\underbrace{11…..1}_{n+1\text{ so }\!\!\acute{\mathrm{a}}\!\!\text{ 1}};\,\,C=\underbrace{66…..6}_{n\text{ so }\!\!\acute{\mathrm{a}}\!\!\text{ 6}}$; với n là số tự nhiên lớn hơn 1.
Chứng minh rằng $A+B+C+8$ là số chính phương.
Lời giải
Ta có $A=\frac{{{10}^{2n}}-1}{9};\,B=\frac{{{10}^{n+1}}-1}{9};\,C=\frac{6\left( {{10}^{n}}-1 \right)}{9}$
Xét $A+B+C+8=$
$\frac{{{10}^{2n}}-1}{9}+\frac{{{10}^{n+1}}-1}{9}+\frac{{{6.10}^{n}}-6.1}{9}+8=\frac{{{10}^{2n}}+{{16.10}^{n}}+64}{9}={{\left( \frac{{{10}^{n}}+8}{3} \right)}^{2}}$
Mà ${{10}^{n}}+8=\underbrace{100..0}_{n-1}8\vdots 3\Rightarrow A+B+C+8$ là số chính phương.