Bạn có tò mò muốn biết đồng dư thức là gì và làm sao để chứng minh chúng một cách nhanh chóng? Đây không chỉ là khái niệm khô khan, mà là chìa khóa giải mã những bài toán số học đầy thách thức. Trong bài viết này, chúng ta sẽ khám phá lý thuyết dễ hiểu, mẹo hay, và bài tập đồng dư thức có lời giải từ khó đến dễ. Hãy sẵn sàng chinh phục cách giải đồng dư thức để trở thành bậc thầy toán học nhé!
1. Đồng dư thức là gì?
Cho số nguyên $m>0$. Nếu hai số nguyên a và b khi chia cho m có cùng số dư thì ta nói a đồng dư với b theo môđun m và ký hiệu: $a\equiv b$ (mod m).
Chú ý:
- $a\equiv b$ (mod m) là một đồng dư thức với a là vế trái, b là vế phải.
- $a\equiv b$ (mod m) $\Leftrightarrow a-b\vdots m\Leftrightarrow \exists t\in z$ sao cho $a=b+mt$
- Nếu a và b không đồng dư với nhau theo môđun m ta ký hiệu:
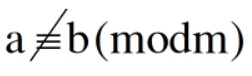
2. Tính chất quan trọng
a) Tính chất phản xạ: $a\equiv a$ (mod m)
b) Tính chất đối xứng: $a\equiv b$ (mod m) $\Rightarrow b\equiv a\,$ (mod m)
c) Tính chất bắc cầu: $a\equiv b$ (mod m); $b\equiv c$ (mod m)$\Rightarrow a\equiv c$ (mod m).
d) Cộng hay trừ từng vế của đồng dư thức có cùng môđun:
- $a\equiv b$ (mod m); $c\equiv d$ (mod m)$\Rightarrow a\pm c\equiv b\pm d$ (mod m)
- Tổng quát: ${{a}_{i}}\equiv {{b}_{i}}$ (mod m), $i=1;2;…;k\Rightarrow {{a}_{1}}\pm \,{{a}_{2}}\pm \,…\pm \,{{a}_{k}}\equiv {{b}_{1}}\pm \,{{b}_{2}}\pm …\pm \,{{b}_{k}}$ (mod m)
e)
- Nhân hai vế của đồng dư thức với một số nguyên: $a\equiv b$ (mod m)$\Rightarrow ka\equiv kb$ (mod m) với $k\in Z$.
- Nhân hai vế và môđun của đồng dư thức với một số nguyên dương: $a\equiv b$ (mod m) $\Rightarrow ka\equiv kb$ (mod m) với $k\in {{N}^{*}}$
f. Nhân từng vế của nhiều đồng dư thức có cùng môđun:
$a\equiv b$ (mod m); $c\equiv d$ (mod m) $\Rightarrow ac\equiv bd$ (mod m)
Tổng quát: ${{a}_{i}}\equiv {{b}_{i}}$ (mod m), $i=1;2;…;k\Rightarrow {{a}_{1}}\,{{a}_{2}}\,…{{a}_{k}}\equiv {{b}_{1}}\,{{b}_{2}}\,…{{b}_{k}}$ (mod m)
g) Nâng hai vế của một đồng dư thức lên cùng một lũy thừa: $a\equiv b$ (mod m) $\Rightarrow {{a}^{k}}\equiv {{b}^{k}}$ (mod m) $(k\in {{N}^{*}})$
h. Nếu hai số đồng dư với nhau theo nhiều môđun thì chúng đồng dư với nhau theo môđun là BCNN của các môđun ấy: $a\equiv b$ (mod mi) $i=1;2;…;k\Rightarrow a\equiv b$ (mod [m1; m2;…;mk])
Đặc biệt nếu (mi; mj) = 1 (i; j = 1; 2; …; k) thì $a\equiv b$ (mod mi) $\Rightarrow a\equiv b$ (mod m1; m2;…;mk)
k. Nếu \[a\equiv b\] (mod m) thì tập hợp các ước chung của a và m bằng tập hợp các ước chung của b và m.
Đặc biệt: $a\equiv b$ (mod m) $\Rightarrow (a,m)=(b,m)$
m. Chia hai vế và môđun của một đồng dư cho một ước dương chung của chúng: $a\equiv b$ (mod m), $k\in UC(a,b,m),k>0\Rightarrow \frac{a}{k}\equiv \frac{b}{k}\left( \bmod \frac{m}{k} \right)$
Đặc biệt: $ac\equiv bc$ (mod m)$\Rightarrow a\equiv b\left( \bmod \,\,\frac{m}{(c,m)} \right)$
3. Một số định lý (ta thừa nhận không chứng minh)
Định lý Fermat bé. Cho a là số nguyên dương và p là số nguyên tố. Khi đó ta luôn có ${{a}^{p}}\equiv a(\bmod \,p)$. Đặc biệt nếu $(a,p)=1$ thì ${{a}^{p-1}}\equiv 1\,(\bmod \,p)$
Định lý Wilson. Với mọi số nguyên tố p thì $(p-1)!\equiv -1(\bmod \,p)$
Định lý Euler. Cho m là số nguyên dương và a là số nguyên tố cùng nhau với m; $\varphi (m)$ là số các số nguyên dương nhỏ hơn m và nguyên tố cùng nhau với m.
Khi đó ${{a}^{\varphi (m)}}\equiv 1(\bmod \,m)$
Chú ý: Nếu số nguyên dương m có dạng phân tích thành thừa số nguyên tố:
$m=p_{1}^{{{\alpha }_{1}}}.p_{2}^{{{\alpha }_{2}}}…..p_{k}^{{{\alpha }_{k}}}$ thì $\varphi (m)=m\left( 1-\frac{1}{{{p}_{1}}} \right)\left( 1-\frac{1}{{{p}_{2}}} \right)…\left( 1-\frac{1}{{{p}_{k}}} \right)$
3. Bài tập
Bài tập 1. Tìm các số nguyên tố p thỏa mãn ${{2}^{p}}+1\vdots p.$
Lời giải
Theo định lý Fermat bé ta có ${{2}^{p}}\equiv 2(\bmod \,p)$ nên nếu ${{2}^{p}}\equiv -1(\bmod \,p)$ thì ta có $3\equiv 0(\bmod \,p)\Rightarrow p=3$
Mặt khác khi \[p=3\] thì ${{2}^{3}}+1=9\equiv 0(\bmod \,3).$ Vậy $p=3$ là số cần tìm.
Bài tập 2. Tìm hai chữ số tận cùng của ${{2011}^{{{2010}^{2009}}}}$
(Đề thi Olympic Toán Singapore năm 2010)
Lời giải
Ta có $2011\equiv 11(\bmod \,100);\,\,{{11}^{2}}\equiv 21(\bmod \,100);\,\,{{11}^{3}}\equiv 31(\bmod \,100);\,\,{{11}^{5}}\equiv 21.31\equiv 51(\bmod \,100)$
$\Rightarrow {{11}^{10}}\equiv {{51}^{2}}\equiv 1(\bmod \,100)$
Ta có ${{2010}^{2009}}\equiv 0(\bmod \,10)\Rightarrow {{2010}^{2009}}=10k(k\in Z)$
$\Rightarrow {{2011}^{{{2010}^{2009}}}}={{2011}^{10k}}\equiv {{11}^{10k}}\equiv {{({{11}^{10}})}^{k}}\equiv 1(\bmod \,100)$ . Do đó hai chữ số tận cùng là số 01.
Bài tập 3: Chứng minh rằng ${{1}^{4k}}+{{2}^{4k}}+{{3}^{4k}}+{{4}^{4k}}$ không chia hết cho 5.
Lời giải
Do 5 là số nguyên tố nên theo Định lý Fermat bé ta có: với a = 1; 2; 3; 4 ta có:
${{a}^{5}}\equiv a(\bmod \,5)\Leftrightarrow {{a}^{4}}\equiv 1(\bmod \,5)\Leftrightarrow {{a}^{4k}}\equiv 1(\bmod \,5).$
Do đó ${{1}^{4k}}+{{2}^{4k}}+{{3}^{4k}}+{{4}^{4k}}\equiv 1+1+1+1\equiv 4(\bmod \,5)$
Chứng tỏ
Bài tập 4. Chứng minh $A={{2012}^{4n}}+{{2013}^{4n}}+{{2014}^{4n}}+{{2015}^{4n}}$ không phải là số chính phương với mọi số nguyên dương n.
(Đề thi tuyển sinh vào lớp 10 chuyên trường ĐHSP TP Hồ Chí Minh, năm học 2015-2016)
Lời giải
$\forall n\in N*$ ta có ${{2012}^{4n}}\equiv 0(\bmod \,2);\,\,\,{{2013}^{4n}}\equiv 1(mod\,2);$
${{2014}^{4n}}\equiv 0(\bmod \,2);\,{{2015}^{4n}}\equiv 1(\bmod \,2).$ Do đó $A\equiv 2\equiv 0(\bmod \,2)$
* Ta lại có $2012\equiv 0(\bmod \,4)\Rightarrow {{2012}^{4n}}\equiv 0(\bmod \,4);$
$2014\equiv 2(\bmod \,4)\Rightarrow {{2014}^{2}}\equiv {{2}^{2}}\equiv 0(\bmod \,4)\Rightarrow {{2014}^{4n}}\equiv {{({{2014}^{2}})}^{2n}}\equiv 0(\bmod \,4)$
Do $2013\equiv 1(\bmod \,4)\Rightarrow {{2013}^{4n}}\equiv 1(\bmod \,4);$
Do $2015\equiv -1(\bmod \,4)\Rightarrow {{2015}^{4n}}={{(-1)}^{4n}}\equiv 1(\bmod \,4)$
Vậy $A\equiv 2(\bmod \,4)$ nghĩa là A chia cho 4 dư 2.
Ta có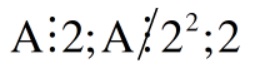 
là số nguyên tố.
Vậy A không là số chính phương $\forall n\in {{N}^{*}}.$
Bài tập 5: Chứng minh rằng với mỗi số nguyên tố p tồn tại vô số số có dạng ${{2}^{n}}-n,(n\in N)$ chia hết cho p.
(Thi vô địch Canada năm 1983).
Lời giải
* Nếu $p=2$ thì ${{2}^{n}}-n\vdots 2,\forall n=2k\,(k\in N)$
* Nếu $p\ne 2$ do $(2;p)=1$ nên theo định lý Fermat bé ta có:
${{2}^{p-1}}\equiv 1(\bmod \,p)\Rightarrow {{2}^{p-1}}-1\equiv 0(\bmod \,p)\Rightarrow {{2}^{{{(p-1)}^{2k}}}}-1\equiv 0(\bmod \,p)$
Hay là ${{2}^{{{(p-1)}^{2k}}}}-1\vdots p\,\,(k\in N;k\ge 2)$
Mặt khác ${{(p-1)}^{2k}}\equiv {{(-1)}^{2k}}\equiv 1(\bmod \,p)$
$\Rightarrow {{2}^{{{(p-1)}^{2k}}}}-{{(p-1)}^{2k}}=\underbrace{\left[ {{2}^{{{(p-1)}^{2k}}}}-1 \right]}_{\vdots p}-\underbrace{\left[ {{(p-1)}^{2k}}-1 \right]}_{\vdots p}\vdots p$
Vậy tồn tại vô số số tự nhiên n có dạng $n={{(p-1)}^{2k}},\,(\forall k\in N;k\ge 2)$ sao cho ${{2}^{n}}-n\vdots p$
Bài tập 6.
a) Với giá trị nào của số tự nhiên n thì ${{3}^{n}}+63$ chia hết cho 72.
b) Cho $A={{20}^{n}}+{{16}^{n}}-{{3}^{n}}-1.$ Tìm giá trị tự nhiên của n để $A\vdots 323$
Lời giải
a) Ta có $72=8.9$ và $(8;9)=1$
* $63\equiv 0(\bmod \,9);$ khi $n=2$ thì ${{3}^{n}}\equiv 0(\bmod \,9)$ do đó ${{3}^{n}}+63\equiv 0(\bmod \,9)$
* Mặt khác, với $n=2k(k\in {{N}^{*}})$ thì ${{3}^{n}}-1={{3}^{2k}}-1={{9}^{k}}-1\equiv {{1}^{k}}-1\equiv 0(mod\,8)$
Do đó ${{3}^{n}}+63={{3}^{n}}-1+64\equiv 0(\bmod \,8)$
Vậy với $n=2k(k\in {{N}^{*}})$ thì ${{3}^{n}}+63\vdots 72$
b) Ta có $323=17.19$ và $(17;19)=1$
* $A=({{20}^{n}}-1)+({{16}^{n}}-{{3}^{n}})=P+Q$
Ta có ${{20}^{n}}\equiv 1(\bmod \,19)\Rightarrow P\equiv 0(\bmod \,19)$
Nếu $n=2k(k\in {{N}^{*}})$ thì $Q={{16}^{2k}}-{{3}^{2k}}\equiv {{(-3)}^{2k}}-{{3}^{2k}}\equiv {{3}^{2k}}-{{3}^{2k}}\equiv 0(\bmod \,19)$
$\Rightarrow A=P+Q\equiv 0(\bmod \,19)$
* $A=({{20}^{n}}-{{3}^{n}})+({{16}^{n}}-1)=P’+Q’$
${{20}^{n}}\equiv {{3}^{n}}(\bmod \,17).$ Do đó $P’={{20}^{n}}-{{3}^{n}}\equiv 0(\bmod \,17)$
Nếu $n=2k(k\in {{N}^{*}})$ thì $Q’={{16}^{2k}}-1={{(-1)}^{2k}}-1\equiv 1-1\text{ }\equiv 0(\bmod \,17)$
$\Rightarrow A=P’+Q’\equiv 0(\bmod \,17).$ Do $(17;19)=1$ nên $A\equiv 0(\bmod \,17.19)$
Vậy với $n=2k(k\in {{N}^{*}})$ thì $A={{20}^{n}}+{{16}^{n}}-{{3}^{n}}-1\vdots 323$
Bài tập 7. Tìm hai chữ số cuối cùng của số $A={{41}^{106}}+{{57}^{2012}}.$
(Đề thi vào lớp 10 trường THPT chuyên KHTN, ĐHQG Hà Nội, năm học 2012-2013)
Lời giải
Ta có ${{41}^{2}}={{(40+1)}^{2}}={{40}^{2}}+80+1\equiv 81(\bmod \,100)$
${{41}^{2}}\equiv {{81}^{2}}\equiv 6561\equiv 61(\bmod \,100)\Rightarrow {{41}^{5}}\equiv 61.41\equiv 1(\bmod \,100)$
$\Rightarrow {{41}^{106}}\equiv 41.{{({{41}^{5}})}^{21}}\equiv 41\text{ }(\bmod \,100)$
Mặt khác ${{57}^{4}}=10556001\equiv 1(\bmod \,100)\Rightarrow {{57}^{2012}}={{({{57}^{4}})}^{503}}\equiv 1(\bmod \,100)$
Vì thế $A\equiv 41+1(\bmod \,100)$
Do đó hai chữ số cuối cùng của số $A={{41}^{106}}+{{57}^{2012}}$ là 42.
Bài tập 8.
a) Chứng minh rằng tổng các bình phương của ba số nguyên trong phép chia cho 8 không thể có dư là 7.
b) Chứng minh phương trình $4{{x}^{2}}+{{y}^{2}}+9{{z}^{2}}=2015$ không có nghiệm nguyên.
Lời giải
a) Giả sử $a,b,c\in Z$ mà ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}\equiv 7(\bmod \,8)$
Ta có $a\equiv 0;\pm 1;\pm 2;\pm 3;4\,\,(\bmod \,8)\Rightarrow {{a}^{2}}\equiv 0;1;4\,(\bmod \,8)$
$\to {{b}^{2}}+{{c}^{2}}\equiv 7;6;3\,(\bmod \,8).$ Điều này vô lý vì ${{b}^{2}}\equiv 0;1;4\,(\bmod \,8)$
Và ${{c}^{2}}\equiv 0\,;1;4(\bmod \,8)\Rightarrow {{b}^{2}}+{{c}^{2}}\equiv 0;1;2;4;5\,(mod\,8)$
Vậy 
b) Áp dụng câu a) ta có với $x,y,z\in Z$
Mà $2015=8.251+7\equiv 7\,(\bmod \,8)$
Vậy phương trình đã cho không có nghiệm nguyên.
Bài tập 9. Tìm tất cả các số nguyên tố p sao cho ${{p}^{2}}+20$ là số nguyên tố.
Lời giải
Với $p=3$ thì ${{p}^{2}}+20=29$ là số nguyên tố.
Với $p\ne 3$ thì ${{p}^{2}}\equiv 1(\bmod \,3)$ nên ${{p}^{2}}+20\equiv 21\equiv 0(\bmod \,3)$
Vậy ${{p}^{2}}+20\vdots 3$ mặt khác ${{p}^{2}}+20>3$ nên ${{p}^{2}}+20$ là hợp số. Vậy chỉ có 1 số nguyên tố cần tìm là $p=3.$
Bài tập 10. Cho p là số nguyên tố. Chứng minh rằng số $a{{b}^{p}}-b{{a}^{p}}\vdots p$ với mọi số nguyên dương a, b.
Lời giải
Với $a,b\in {{N}^{*}}$ . Nếu \[ab\vdots p\] thì số $a{{b}^{p}}-b{{a}^{p}}\vdots p$
Nếu 
thì $(a,p)=(b,p)=1.$
Do đó ${{a}^{p-1}}\equiv {{b}^{p-1}}\equiv 1(mod\,p)\Rightarrow {{a}^{p-1}}-{{b}^{p-1}}\equiv 0(mod\,p)\Rightarrow ab({{a}^{p-1}}-{{b}^{p-1}})\equiv 0(\bmod \,p)$
$\Rightarrow a{{b}^{p}}-b{{a}^{p}}\equiv 0(\bmod \,p)$ hay $a{{b}^{p}}-b{{a}^{p}}\vdots p,\forall a,b\in {{N}^{*}}.$
Bài tập 11. Cho biểu thức $A=\left( {{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}} \right)-\left( {{a}^{2008}}+{{b}^{2008}}+{{c}^{2008}} \right)$ với a, b, c là các số nguyên dương. Chứng minh rằng A chia hết cho 30.
(Đề thi chọn học sinh giỏi môn toán lớp 9 TP. Hà Nội, năm học 2011-2012)
Lời giải
Bài toán có nhiều cách giải. Sau đây là cách giải theo đồng dư thức:
* Ta có $\forall n\in {{N}^{*}}$ thì ${{n}^{5}}-n\equiv 0(mod\,30)$ (ví dụ 8 chuyên đề 26 đã chứng minh)
$\begin{align} & A=({{a}^{2012}}-{{a}^{2008}})+({{b}^{2012}}-{{b}^{2008}})+({{c}^{2012}}-{{c}^{2008}}) \\ & A={{a}^{2007}}({{a}^{5}}-a)+{{b}^{2007}}({{b}^{5}}-b)+{{c}^{2007}}({{c}^{5}}-c) \\ \end{align}$
Ta có ${{a}^{5}}-a\equiv 0(\bmod \,30)\Rightarrow {{a}^{2007}}({{a}^{5}}-a)\equiv 0(\bmod \,30)$
Tương tự ${{b}^{2007}}({{b}^{5}}-b)\equiv 0(mod\,30);\,{{c}^{2007}}({{c}^{5}}-c)\equiv 0(\bmod \,30)$
Vậy \[A\equiv 0(\bmod \,30).\] Hay $A\vdots 30$
Bài tập 12. Chứng minh rằng không tồn tại các bộ ba số nguyên (s; y; z) thỏa mãn đẳng thức ${{x}^{4}}+{{y}^{4}}=7{{z}^{4}}+5.$
(Đề thi vào lớp 10 trường THPT chuyên KHTN, ĐHKHTN, ĐHQG Hà Nội, năm học 2011-2012)
Lời giải
Giả sử tồn tại bộ ba số nguyên (x; y; z) thỏa mãn ${{x}^{4}}+{{y}^{4}}=7{{z}^{4}}+5$
$\Leftrightarrow {{x}^{4}}+{{y}^{4}}+{{z}^{4}}=8{{z}^{4}}+5\,\,\,\,\,\,\,(1)$
Xét với một số nguyên a bất kỳ thì nếu a chẵn thì $a=2k(k\in Z)$ $\Rightarrow {{a}^{4}}=16{{k}^{4}}\equiv 0(\bmod \,8);$
Nếu a lẻ thì ${{a}^{4}}={{(2k+1)}^{4}}\equiv 1(\bmod \,8)$
Do đó ${{x}^{4}}+{{y}^{4}}+{{z}^{4}}\equiv 0;1;2;3(\bmod \,8).$ Trong khi đó $8{{z}^{4}}+5\equiv 5(\bmod \,8)$ mâu thuẫn với (1). Vậy không tồn tại các bộ ba số nguyên (s; y; z) thỏa mãn đẳng thức ${{x}^{4}}+{{y}^{4}}=7{{z}^{4}}+5$
Bài tập 13. Cho a, b là hai số nguyên dương thỏa mãn $a+20$ và $b+13$ cùng chia hết cho 21. Tìm số dư trong phép chia $A={{4}^{a}}+{{9}^{b}}+a+b$ cho 21.
(Đề thi tuyển sinh lớp 10 THPT chuyên Trần Phú – Hải Phòng, năm học 2013-2014)
Lời giải
Do $a+20\vdots 21\Rightarrow a\equiv 1(\bmod 3)$và $a\equiv 1(\bmod 7)$
$b+13\vdots 21\Rightarrow b\equiv 2(\bmod \text{3) }$và $b\equiv 2(\bmod 7)$
Suy ra $A={{4}^{a}}+{{9}^{b}}+a+b\equiv 1+0+1+2\equiv 1(\bmod 3)\Rightarrow A\equiv 10(\bmod 3)$
Xét $a=3k+1;b=3q+2$với $k,q\in N$ta có ${{4}^{a}}={{4}^{3k+1}}={{4.64}^{k}}\equiv 4(\bmod 7)$
${{9}^{b}}={{9}^{3q+2}}\equiv {{2}^{3q+2}}\equiv {{4.8}^{q}}\equiv 4(\bmod 7)$
Do đó $A={{4}^{a}}+{{9}^{b}}+a+b\equiv 4+4+1+1\equiv 10(\bmod 7)\Rightarrow A\equiv 10(\bmod 7)$
$A\equiv 10(\bmod 3)$và$A\equiv 10(\bmod 7)$mà $(3;7)=1$nên $A\equiv 10(\bmod 3.7)$
Hay $A\equiv 10(\bmod 21)$. Vậy số dư trong phép chia A cho 21 là 10.
Bài tập 14. Cho n là một số nguyên dương chứng minh $A={{2}^{3n+1}}+{{2}^{3n-1}}+1$ là hợp số.
(Đề thi học sinh giỏi lớp 9 TP. Hà Nội, năm học 2014-2015)
Lời giải
${{2}^{3}}\equiv 1(mod\,7)\Rightarrow {{({{2}^{3}})}^{n}}\equiv 1(\bmod \,7)\Rightarrow {{2}^{3n+1}}=2.{{({{2}^{3}})}^{n}}\equiv 2(\bmod \,7)$
và ${{2}^{3n-1}}={{2}^{2}}.{{({{2}^{3}})}^{n-1}}\equiv 4(\bmod \,7)$
nên $A\equiv 2+4+1\equiv 0(\bmod \,7)$ nghĩa là $A\vdots 7$ . Mà với $n\in {{N}^{*}}$ thì A>7.
Vậy A là hợp số.