7 Hằng Đẳng Thức Đáng Nhớ Là Gì?
7 hằng đẳng thức đáng nhớ là những công thức toán học cơ bản và quan trọng nhất trong chương trình Đại số lớp 8. Đây là nền tảng giúp học sinh giải quyết các bài toán phân tích đa thức thành nhân tử, rút gọn biểu thức và tính toán nhanh chóng.

Hằng đẳng thức đáng nhớ là những đẳng thức đúng với mọi giá trị của biến, được sử dụng rộng rãi trong toán học từ cấp THCS đến đại học. Việc nắm vững 7 hằng đẳng thức cơ bản sẽ giúp các em:
Lợi ích khi học thuộc 7 hằng đẳng thức:
- ✅ Giải toán nhanh và chính xác hơn
- ✅ Phân tích đa thức thành nhân tử một cách hiệu quả
- ✅ Rút gọn biểu thức phức tạp
- ✅ Làm nền tảng cho các kiến thức toán học nâng cao
- ✅ Tính nhẩm các phép toán phức tạp
7 Hằng Đẳng Thức Đáng Nhớ Lớp 8 Chi Tiết
1. Hằng đẳng thức thứ nhất: Bình phương của tổng

• (x + 3)² = x² + 6x + 9
• (2a + 5)² = 4a² + 20a + 25
2. Hằng đẳng thức thứ hai: Bình phương của hiệu
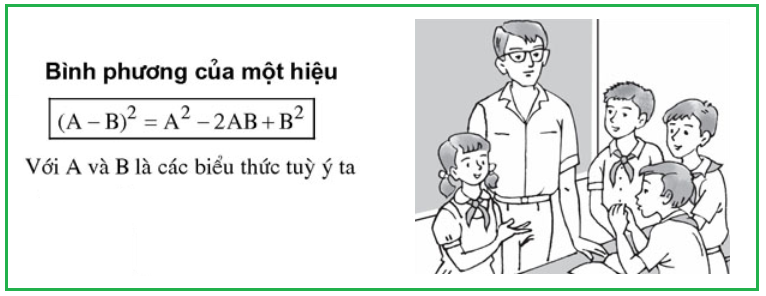
• (x – 4)² = x² – 8x + 16
• (3y – 2)² = 9y² – 12y + 4
3. Hằng đẳng thức thứ ba: Hiệu hai bình phương
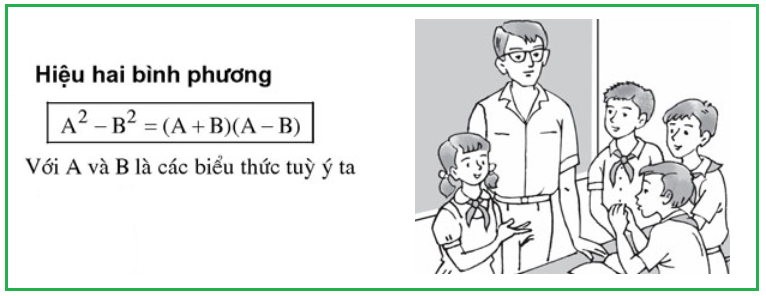
• x² – 9 = (x + 3)(x – 3)
• 16y² – 25 = (4y + 5)(4y – 5)
4. Hằng đẳng thức thứ tư: Lập phương của tổng
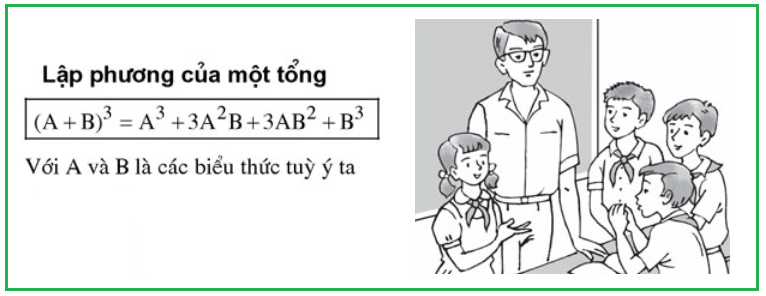
• (x + 2)³ = x³ + 6x² + 12x + 8
• (a + 1)³ = a³ + 3a² + 3a + 1
5. Hằng đẳng thức thứ năm: Lập phương của hiệu
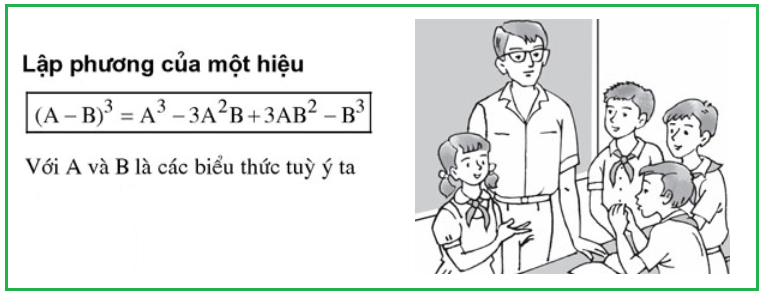
• (x – 3)³ = x³ – 9x² + 27x – 27
• (2y – 1)³ = 8y³ – 12y² + 6y – 1
6. Hằng đẳng thức thứ sáu: Tổng hai lập phương

• x³ + 8 = (x + 2)(x² – 2x + 4)
• 27a³ + b³ = (3a + b)(9a² – 3ab + b²)
7. Hằng đẳng thức thứ bảy: Hiệu hai lập phương
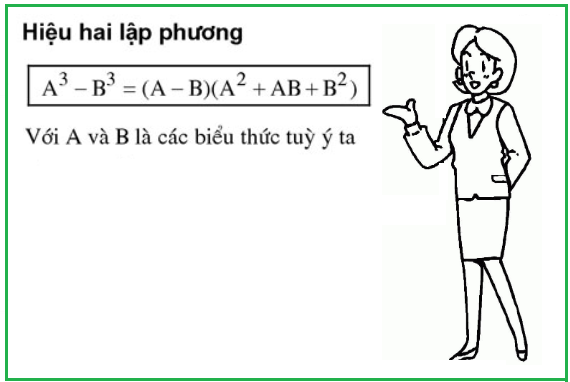
• x³ – 27 = (x – 3)(x² + 3x + 9)
• 8y³ – 1 = (2y – 1)(4y² + 2y + 1)
Bảng Tóm Tắt 7 Hằng Đẳng Thức Đáng Nhớ
| STT | Tên hằng đẳng thức | Công thức |
|---|---|---|
| 1 | Bình phương tổng | (a + b)² = a² + 2ab + b² |
| 2 | Bình phương hiệu | (a – b)² = a² – 2ab + b² |
| 3 | Hiệu hai bình phương | a² – b² = (a + b)(a – b) |
| 4 | Lập phương tổng | (a + b)³ = a³ + 3a²b + 3ab² + b³ |
| 5 | Lập phương hiệu | (a – b)³ = a³ – 3a²b + 3ab² – b³ |
| 6 | Tổng hai lập phương | a³ + b³ = (a + b)(a² – ab + b²) |
| 7 | Hiệu hai lập phương | a³ – b³ = (a – b)(a² + ab + b²) |
Mẹo Ghi Nhớ 7 Hằng Đẳng Thức Hiệu Quả
Phương pháp ghi nhớ bằng câu thơ
Tích hai bình phương hiệu liền.
Lập phương tổng, lập phương hiệu,
Tổng hiệu lập phương theo sau.”
Mẹo nhớ từng công thức:
- HĐT 6-7: “Bình phương thiếu” – thiếu dấu nhân ở giữa
Cách nhớ qua hình ảnh trực quan
Liên tưởng hình học:
- Bình phương: Hình vuông có cạnh (a+b) hoặc (a-b)
- Lập phương: Hình khối có cạnh (a+b) hoặc (a-b)
- Hiệu hai bình phương: Hai hình vuông bị cắt bỏ
Bài Tập Thực Hành 7 Hằng Đẳng Thức
Dạng 1: Khai triển biểu thức
a) (x + 7)²
b) (2y – 3)²
c) (a + b)³
Lời giải:
a) (x + 7)² = x² + 14x + 49
b) (2y – 3)² = 4y² – 12y + 9
c) (a + b)³ = a³ + 3a²b + 3ab² + b³
Dạng 2: Phân tích thành nhân tử
a) x² – 49
b) 8a³ – 1
c) x³ + 125
Lời giải:
a) x² – 49 = x² – 7² = (x + 7)(x – 7)
b) 8a³ – 1 = (2a)³ – 1³ = (2a – 1)(4a² + 2a + 1)
c) x³ + 125 = x³ + 5³ = (x + 5)(x² – 5x + 25)
Dạng 3: Tính nhanh
a) 48²
b) 102³
c) 99² – 1²
Lời giải:
a) 48² = (50 – 2)² = 50² – 2×50×2 + 2² = 2500 – 200 + 4 = 2304
b) 102³ = (100 + 2)³ = 100³ + 3×100²×2 + 3×100×2² + 2³ = 1061208
c) 99² – 1² = (99 + 1)(99 – 1) = 100 × 98 = 9800
Muốn làm thêm bài tập?
Tải ngay bộ 100+ bài tập 7 hằng đẳng thức đáng nhớ có lời giải chi tiết!
Tải bài tập miễn phíỨng Dụng Thực Tế của 7 Hằng Đẳng Thức
Trong tính toán nhanh
- Tính nhẩm: 103² = (100 + 3)² = 100² + 2×100×3 + 3² = 10609
- Tính hiệu: 50² – 48² = (50 + 48)(50 – 48) = 98×2 = 196
- Tính tích: 99 × 101 = (100-1)(100+1) = 100² – 1² = 9999
Trong giải phương trình
- Phương trình bậc 2: x² – 9 = 0 ⟹ (x – 3)(x + 3) = 0
- Phương trình bậc 3: x³ – 8 = 0 ⟹ (x – 2)(x² + 2x + 4) = 0
Trong rút gọn biểu thức
Việc sử dụng hằng đẳng thức giúp rút gọn các biểu thức phức tạp thành dạng đơn giản hơn, dễ tính toán và phân tích.
Lỗi Sai Thường Gặp và Cách Khắc Phục
⚠️ Những lỗi sai phổ biến:
- Quên hệ số 2: (a + b)² ≠ a² + b² (thiếu 2ab)
- Nhầm lẫn dấu: (a – b)² ≠ a² + 2ab + b²
- Quên “bình phương thiếu”: a³ + b³ ≠ (a + b)(a² + b²)
- Nhầm hệ số 3: (a + b)³ ≠ a³ + a²b + ab² + b³
💡 Cách khắc phục:
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau
- Ghi nhớ qua câu thơ và các mẹo đã nêu
- Kiểm tra lại bằng cách khai triển ngược
- Làm bài tập từ dễ đến khó để củng cố kiến thức
Câu Hỏi Thường Gặp (FAQ)
Vì đây là 7 công thức cơ bản nhất, được sử dụng thường xuyên trong toán học và cần được ghi nhớ thành thạo. Chúng là nền tảng cho việc học toán ở các cấp độ cao hơn.
Có thể sử dụng câu thơ ghi nhớ, luyện tập thường xuyên và hiểu rõ ý nghĩa của từng công thức. Quan trọng nhất là phải hiểu logic của từng công thức chứ không chỉ học thuộc máy móc.
Có, hằng đẳng thức là nền tảng cho nhiều chủ đề toán THPT như đạo hàm, tích phân, phương trình bậc cao, bất đẳng thức và nhiều lĩnh vực khác.
Cần hiểu logic của từng công thức và luyện tập đều đặn. Chú ý đặc biệt đến các dấu âm, hệ số và cách sắp xếp các số hạng. Có thể vẽ sơ đồ hoặc dùng màu sắc để phân biệt.
Có nhiều hằng đẳng thức khác như hằng đẳng thức Sophie Germain, các hằng đẳng thức bậc cao hơn, nhưng 7 hằng đẳng thức này là cơ bản và quan trọng nhất cho học sinh THCS.
Có, việc học thuộc lòng là rất cần thiết vì chúng được sử dụng thường xuyên trong giải toán. Tuy nhiên, quan trọng hơn là hiểu rõ cách suy luận và áp dụng của từng công thức.
Sử dụng khi gặp biểu thức có dạng a² – b². Đây là công thức phân tích nhân tử rất hữu ích để giải phương trình, rút gọn phân số và tính toán nhanh.
“Bình phương thiếu” là cách gọi tắt cho biểu thức a² ∓ ab + b². Gọi là “thiếu” vì không có dấu cộng ở giữa như bình phương đầy đủ (a ± b)².
Dùng công thức thuận khi cần khai triển (từ dạng thu gọn ra dạng khai triển). Dùng công thức nghịch khi cần phân tích thành nhân tử hoặc rút gọn (từ dạng khai triển về dạng thu gọn).
Vì đây là khai triển lập phương (bậc 3). Theo công thức nhị thức Newton, hệ số được tính theo tổ hợp C(3,1) = 3 và C(3,2) = 3.
Có, hằng đẳng thức áp dụng với mọi số thực, kể cả số âm. Ví dụ: (-3 + 2)² = (-1)² = 1, và theo công thức: (-3)² + 2×(-3)×2 + 2² = 9 – 12 + 4 = 1.
Có, (a+b)² có thể hiểu như diện tích hình vuông cạnh (a+b), còn a²-b² có thể hiểu như hiệu diện tích hai hình vuông. Điều này giúp visualize và hiểu sâu hơn về công thức.
Có thể thay số cụ thể vào biến để kiểm tra, hoặc khai triển ngược lại từ kết quả. Ví dụ: nếu có (x+2)² = x² + 4x + 4, thay x = 1 sẽ được 9 = 1 + 4 + 4 = 9 ✓
Hằng đẳng thức xuất hiện trong hầu hết các kỳ thi từ kiểm tra 15 phút đến thi học kỳ, thi vào lớp 10, và cả thi đại học. Đây là kiến thức nền tảng không thể thiếu.
🎯 Thành Thạo 7 Hằng Đẳng Thức Ngay Hôm Nay!
Đừng để kiến thức toán học trở thành rào cản. Với phương pháp học đúng và luyện tập đều đặn, bạn sẽ nắm vững 7 hằng đẳng thức đáng nhớ một cách dễ dàng!
Bắt đầu học ngay Tải phiếu bài tậpĐang tải tài liệu…